希望各位讀者在昨天經歷過Binary Search的摧殘後還能保有一定的熱忱往下學習。我之所以會在資料結構的篇幅中可以安排一個Binary Search是因為有一些資料結構操作上的時間複雜度會涉及到log n，但大家也不用擔心，因為其實跟log n有關係的很多都跟樹有關，又或者我們可以映射到樹的觀念來去理解他。

今天的主題是Heap，這個Heap跟我們電腦所說的Memory Heap是不一樣的喔，我們今天說的Heap是一種資料結構。至於這個Heap有甚麼特別的地方就讓我們繼續往下看吧。

Heap其實就是一種特別的Binary Tree，他的特性就是他能夠保持他Root的值是整個Heap裡最大(或最小)的值，我們分別稱呼他Max Heap跟Min Heap，這樣的特性又可以延伸到每一個子樹，所以我們會發現，每一個子樹的root node的值都會是那個樹裡最大(或最小)的。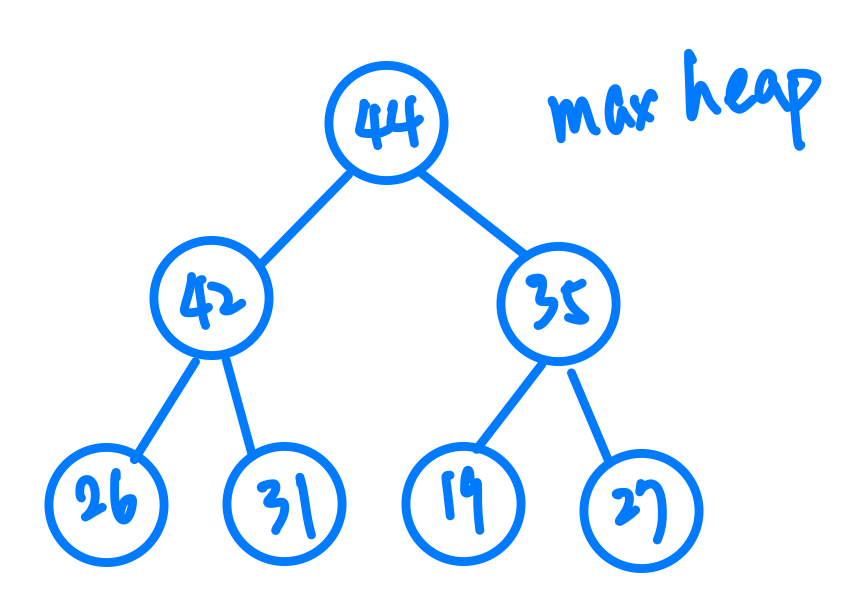

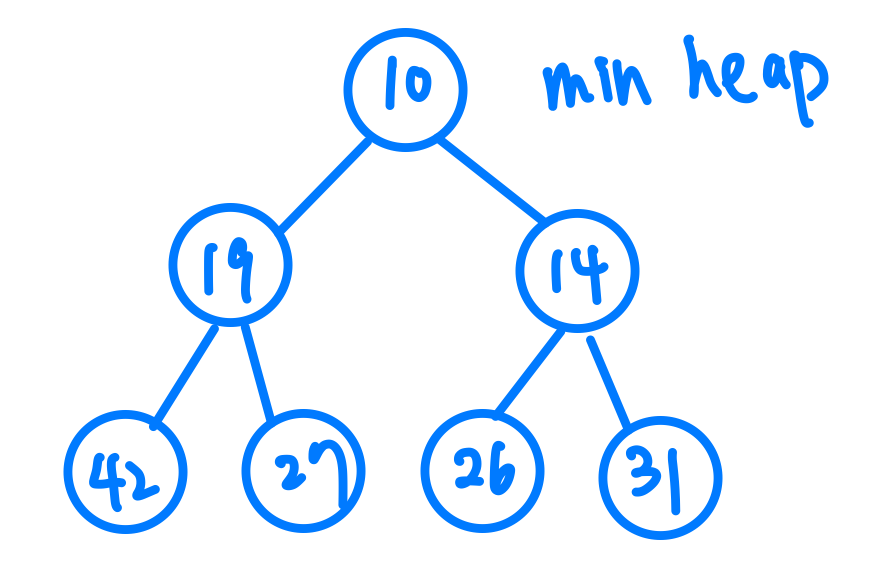
我們可以取出 Heap裏頭最上面的值(前面所提到最大或最小)，經過Heap的自動調整，root上依然是整個Heap最大的值，我們也可以插入一個新的值，Heap也能夠幫我們自動調整為root上會是最大的值。這邊我不會講太多關於Heap怎麼去調整的細節，大家唯一要記住的是，它調整的時間複雜度是log n(大致上就是，我最差的情況下，會從最底的節點比較到最高的節點，如果我底的節點比較大，我就會移上來，那我最多也只會比較「樹的高度」那麼多次。)，另外如果我要重頭建一個Heap，在Python裡頭叫Heapify，我們在O(n)的時間就可以把他建起來囉！好的Heap的重點差不多講完了。

Heap有甚麼好處嗎？

聽完Heap的介紹後，好像還不是很能懂Heap到底實用在哪裡，如果我要找最大值，我在O(n)的時間內就可以找到了，如果我要找第K大的值，我只要先排序(後面篇幅會講到)再用index去找，這樣時間複雜度也才O(n log n)。

沒有錯沒有錯，其實Heap在很多時候，它的用途真的會有一點難去應用，但我在這邊要給各位讀者一個想法，我們不仿先記著，之後有遇到所說的情況再回頭看。
Heap擅長的是處理動態的「資料流」，甚麼意思？想像今天如果已經有一個排序好的Array我們要再插入一個值，但是我們還是要讓他保持整個Array是排序過的狀態，我們勢必要花O(n)的時間才能確定他要插入在哪裡，但是Heap不用，Heap只需要花O(log n)的時間就可以將新的值插入到Heap中，但是當然我排序過的Array要取出最大值或最小值只需要O(1)，相反的我的Heap卻要O(log n)，所以說有時候資料結構的使用還是必須看過Case後再去決定才會有比較好的效果呦！